遺伝学では確率と統計が頻繁に使われます。大学で遺伝学や分子生物学を学ぶ人が絶対に知っておきたい数学的手法をまとめてみました!
加法定理
加法定理は背反である遺伝交配における計算で使われます。背反であるというのは、ある複数の結果が同時に起こることができないときのことです。これは「相互に背反」と言ったりもしますが、これは以下のような場合です。
この場合、1だけが男の子になる確率は1/8、2人が男の子になる確率は3/8、3人とも男の子になる確率は3/8、1人も男の子が生まれない(全員が女の子)確率は1/8となります。
そして、これらの確率はすべて足せば1になります。1/8 + 3/8 + 3/8 + 1/8 = 1ですね。
少なくともひとり男の子が生まれる確率は1- 1/8 = 7/8と計算することができます。
いまはさらっと「男の子が2人、または3人生まれる確率は3/8」といってしまったのですが、ではこの確率はどのようにして求めることができるのでしょうか。

この場合は乗法定理を使います!
乗法定理
乗法定理はお互いに独立な遺伝交配で起こる確率を求める場合に用いられます。
「独立」しているとは、ひとつの事象が起こるときに、それがほかの事象が起きるか否かに何の影響も与えないときのことです。
この場合、3人目の子供の性別が男になるか女になるかは、先に生まれた2人の子供の性別によって影響はされません。先に生まれた子どもがすべて男の子であろうと、すべて女の子であろうと、男女ひとりずつだろうと、3人目の男の子が生まれる確率は1/2で、女の子が生まれる確率も1/2です。これが互いに独立であるということです。
独立であるときには、ある事象が生じる確率はそれぞれの確率の積に等しくなります。
3人すべて男の子が生まれる確率は、1/2 × 1/2 × 1/2 = 1/8となります。
遺伝学では加法定理と乗法定理を組み合わせて確率を求める
遺伝学では加法定理と乗法定理を同時に使うことが多くなります。
3人の子供が全員男の子である確率は1/8でした。3人すべてが女の子となる確率も1/8です。これらの確率は互いに背反です。つまり、3人の子どもが3人とも女性でかつ3人とも男性であることはありえません。なので、生まれる子どもの3人ともが女性、または3人ともが男性である確率はそれぞれの確率の和となります。
1/8 + 1/8 = 1/4

では、他のパターンも考えてみましょう!
この場合は、生まれる順序を考えなくてはいけません。男2人・女1人の場合、起こる可能性のある順序には、
男男女 男女男 女男男
3通りがあって、それぞれの確率は1/8です。
加法定理を用いると、1/8 + 1/8 + 1/8 となり、つまり3/8が男2人・女1人が生まれる確率です。また同様に、男1人・女2人の場合も3/8となります。
なので、上の問題の答えは3/8 + 3/8 = 3/4となります。
(p+q)nを使って確率を求める

数式が出てきたので、数学が苦手な人は「うわ…」と思ったかもしれませんが、簡単なのでついてきてください!
(p+q)nという二項式は確率の計算にとっても便利です。
子どもの性別を求めたかったら、男の子が生まれる確率をp、女の子が生まれる確率をq、子供の数をnに当てはめることで計算できます。子どもが3人の場合は、この二項式を展開すると、
(p+q)₃ = p³ + 3p²q + 3pq² + p³
となるので、男1人・女2人の確率が知りたい場合は、pq²の項に数字を当てはめればよいのです。
3pq² = 3(1/2)(1/2)² = 3/8
5人の子供をもつ家族での性比のっかうりつの二項分布は次のようになる。

では、子どもが5人いて、男3人・女2人になる確率はどうなるでしょうか?
(p+q)⁵=1p⁵+5p⁴q+10p³q²+10p²q³+5p⁴q+1q⁵
この展開式を用いると、簡単に求められますね。
10p³q² = 10(1/2)³(1/2)² = 5/16
パスカルの三角形

「(p+q)⁵の展開なんてできない!」と思った方に朗報です!
二項式(p+q)nを展開して係数を求める方法は、実はとっても簡単なんです!
下のような数字が並んだ三角形のことを「パスカルの三角形」とよばれています。
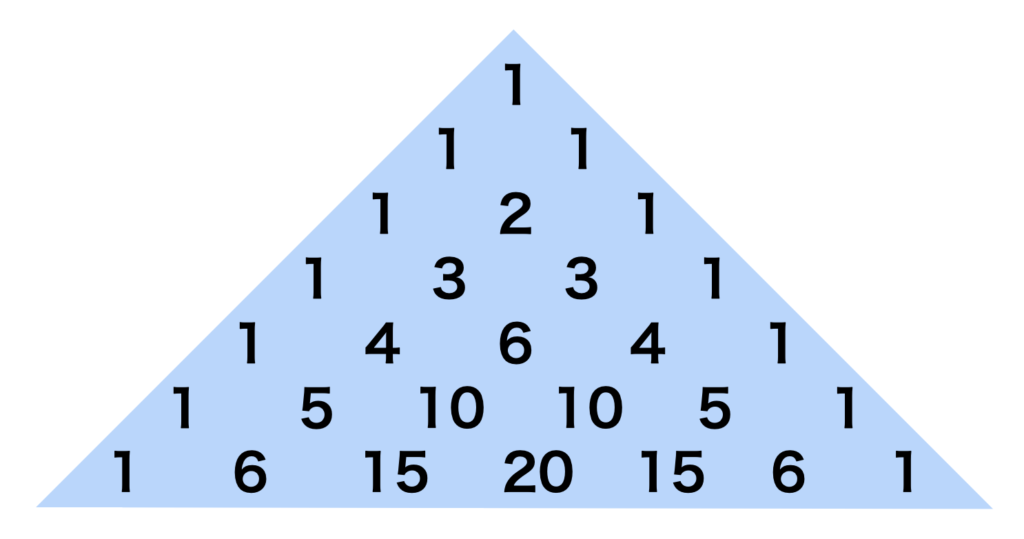
パスカルの三角形は、三角形の左右の辺(等辺)に1が並べられ、それ以外の場所には上の行の両側の2つの数を足した数が並べられている三角形のことです。
このパスカルの三角形の数列は、二項式(p+q)nを展開したときの各項の係数となるのです!
上から3列目の段は「1・2・1」となっていますね。これは、(p+q)²を展開した(p+q)² = p²+2pq+q²の係数に一致します。
(p+q)⁵=1p⁵+5p⁴q+10p³q²+10p²q³+5p⁴q+1q⁵だったら、上から6段目の数列を見てください。係数は「1・5・10・10・5・1」になっていますね!
展開した項のpとqの指数に関しては、第一項はnと同じ数字で、それから1ずつ最終項の0まで減少していきます。qの指数に関してはpとは逆で、第一項の0から1ずつ増加して、最終項はnになります。わかりやすい(p+q)²で考えてみると、
(p+q)² = p²q⁰ + 2p¹q¹ + p⁰q²
n=2の二項式のpの指数は左から「2・1・0」、qの指数は「0・1・2」となっています。
階乗の使い方
順序を考えない場合の確率を求める場合、階乗を使っても計算ができます。次のようなケースを考えてみましょう。
この場合、生まれる順番は関係ないですよね。また、人の場合として考えても、ある夫婦の5人の子どもの性別が男3人・女2人になる確率を求める場合は、1人目は女、2人目は男…と考えなくてもよいことになります。
階乗は「与えられた数から1までのすべての整数の積」という意味です。例えば、
6!= 6 × 5 × 4 × 3 × 2 × 1
という計算をすることになります。

数学では「!」は「びっくりマーク」ではなく、「階乗」と読まれます。
組み合わせの数は全体の数を、順番を考えない重複している事象の数で割って求めることができます。男3人・女2人・計5人の場合、
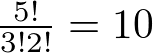
という計算で組み合わせの数が求められます。これは、パスカルの三角形を使ったときの係数と一致していますね!

以上のことから、確率を求めるための次のような一般項を導くことができます。
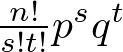

この一般項を使う場合は、n=s+t、そしてp+q=1になります。
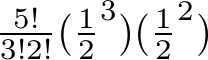
この式を計算すると、同様に5/16となるはずです。

